
Odd Weird Search
Recherche de nombres étranges impairs
URL du projet : http://www.rechenkraft.net/yoyo
Applications : Windows et Linux 64 bits
|
Liens du Projet
|
L'Alliance Francophone
|
Statistiques
|
|
Administré par Yoyo et l'équipe allemande Rechenkraft.net, yoyo@home est une plateforme multi-projets qui permet de faire fonctionner des programmes de recherches extérieurs à BOINC. Pour ce faire, Yoyo et son équipe de programmeurs adaptent les applications au format BOINC.
Outre celui-ci, yoyo@home permet pour le moment de participer au choix à d'autres projets tels que Evolution@home (l'évolution des espèces), Muon (accélérateur de particules partagé), ECM (factorisation en courbe elliptique de Lenstra pour trouver des facteurs de différents nombres) ou encore OGR-27 (déterminer la façon optimale de placer 27 marques selon la règle de Golomb).
Le choix des projets s'effectue sur la page de votre compte dans vos préférences Yoyo@home > (appuyer sur Edit yoyo@home preferences, puis cocher ou décocher les cases à souhait).
 Odd Weird Search est le projet de la théorie des nombres qui recherche des nombres étranges.
Odd Weird Search est le projet de la théorie des nombres qui recherche des nombres étranges.
Qu'est ce qu'un nombre étrange ?
Pour un entier naturel N, si la somme de tous ses diviseurs (y compris 1 mais pas N) est plus grande que lui, alors il est appelé "nombre abondant".
Par exemples:
- 8 n'est pas un nombre abondant car ses diviseurs (1, 2 et 4) dont la somme qui vaut 1+2+4 = 7 est inférieur à 8.
- 12 est un nombre abondant car la somme de ses diviseurs qui vaut 1+2+3+4+6 = 16 est supérieur à 12.
Un nombre abondant est un nombre étrange si aucune somme de ses diviseurs est égale à lui même.
Par exemples:
- 12 est abondant mais pas étrange car 1+2+3
+4+6 = 12. - 70 est un nombre étrange (le plus petit) car la somme de ses diviseurs vaut 1+2+5+7+10+14+15 = 74 (74>70) et aucune somme de ses diviseurs ne vaut 70 (il faudrait retrancher 4 à la somme de ses diviseurs mais 4 est impossible à produire avec ceux-ci).
Une page de l'OEIS (On-Line Encyclopedia of Integer Sequences) est consacrée à ces nombres étranges. Elle contient une liste des nombres étranges connus. Il est à noter que chaque nombre dans la liste est pair.
En fait, aucun nombre étrange impair est connu. Les précédents efforts de recherche ont été menés jusqu'à 1017. Le grand mathématicien Paul Erdos a offert une récompense de 10$ pour la découverte d'un nombre étrange impair et de 25$ pour la démonstration de 'absence de nombre étrange impair. On en déduit qu'Erdos pensait qu'il était plus probable qu'ils existent et que le problème était suffisamment intéressant pour promettre une récompense !
Il a été montré qu'une infinité de nombres étranges existe. Le fait que la suite de nombres étranges a une densité asymptotique (en) positive a aussi été démontré.
En 2012, aucun nombre étrange impair n'a encore été découvert. S'il en existe, ils doivent être plus grands que 232 ≈ 4 × 109. Stanley Kravitz a démontré que si  est un entier strictement positif, si
est un entier strictement positif, si  est un nombre premier et si
est un nombre premier et si 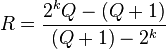 est aussi un nombre premier, alors l'entier
est aussi un nombre premier, alors l'entier  est un nombre étrange.
est un nombre étrange.
À l'aide de cette formule, il a trouvé le plus grand nombre étrange connu actuellement :
Le projet poursuit l'effort de recherche des numéros étranges impairs jusqu'à 1020 ou 3.1020, ou même 1021. Le temps CPU pour tester jusqu'à 1020 serait d'environ 26,3 années, y compris le facteur de duplication des résultats pour vérification.
Sources:
- http://fr.wikipedia.org/wiki/Nombre_%C3%A9trange
- https://www.rechenkraft.net/wiki/index.php?title=Odd_Weird_Search/en





